§7.8
空间直线及其方程
一 空间直线的一般方程
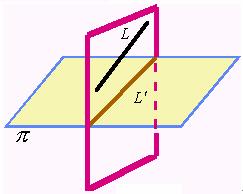
空间直线![]() 可看成两平面
可看成两平面![]() 和
和![]() 的交线。事实上,若两个相交的平面
的交线。事实上,若两个相交的平面![]() 和
和![]() 分别为
分别为
![]()
和 ![]()
那么空间直线![]() 上的任何一点的坐标同时满足这两个平面方程,即应满足方程组
上的任何一点的坐标同时满足这两个平面方程,即应满足方程组
 (1)
(1)
反过来,如果点不在直线![]() 上,那么它不可能同时在平面
上,那么它不可能同时在平面![]() 和
和![]() 上,所以它的坐标不满足方程组(1)。
上,所以它的坐标不满足方程组(1)。
因此,![]() 可用方程组(1)表示,方程组(1)叫做空间直线的一般方程。
可用方程组(1)表示,方程组(1)叫做空间直线的一般方程。
一般说来,过空间一直线的平面有无限多个,所以只要在无限多个平面中任选其中的两个,将它们的方程联立起来,就得到了空间直线的方程。
二 空间直线的对称式方程和参数方程
若一非零向量平行于一条已知直线,这个向量就称之该直线的方向向量。显然,直线上的任何向量均平行于直线的方向向量。
我们知道,过空间一点可作而且只能作一条直线平行于一已知直线,因此,当直线![]() 上的一点
上的一点![]() 和它的一个方向向量
和它的一个方向向量![]() 给定之后,空间直线
给定之后,空间直线![]() 的位置就完全确定下来了。
的位置就完全确定下来了。
下面,我们来建立这种直线的方程。
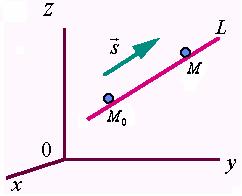
设![]() 是直线
是直线![]() 上的任一点,则
上的任一点,则 ![]() ,而
,而
![]()
故 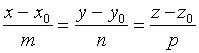 (2)
(2)
反过来,如果点![]() 不在直线
不在直线![]() 上,则
上,则![]() 与
与![]() 不平行,从而(2)式不成立。
不平行,从而(2)式不成立。
因此,方程组(2)就是直线![]() 的方程。称此方程为直线的对称式方程。
的方程。称此方程为直线的对称式方程。
直线的任一方向向量![]() 的坐标
的坐标![]() 叫做该直线的一组方向数,而它的方向余弦叫做该直线的方向余弦。
叫做该直线的一组方向数,而它的方向余弦叫做该直线的方向余弦。
如设 
则  (3)
(3)
方程组(3)叫做直线的参数方程。
【例1】用对称式方程及其参数方程表示直线
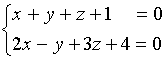
解:先找出这直线上的一点![]() ,如:取
,如:取 ![]() 代入方程组得
代入方程组得
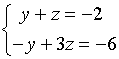
解此二元一次方程组得
![]()
于是,得到直线上的一点
![]() 。
。
再找该直线的一个方向向量![]() ,由于两平面的交线与两平面的法线向量
,由于两平面的交线与两平面的法线向量
![]()
都垂直,可取
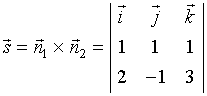
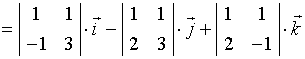
![]()
因此,所给直线的对称式方程为
![]()
直线的参数方程为
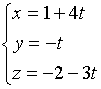
三
两直线的夹角
两直线的方向向量的夹角叫做两直线的夹角。
设有直线![]()

和直线![]()
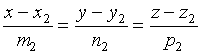
![]() 的方向向量
的方向向量 ![]()
![]() 的方向向量
的方向向量 ![]()
两直线的夹角![]() 的余弦便是两方向向量夹角的余弦。
的余弦便是两方向向量夹角的余弦。
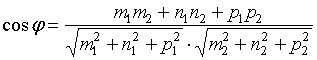 (4)
(4)
由(4)式有
1、![]()
2、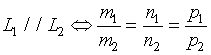
四
直线与平面的夹角
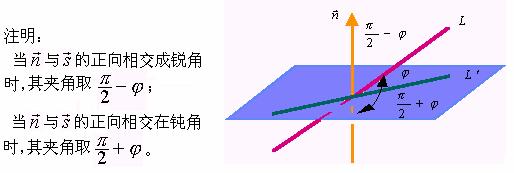
直线和它在平面的投影直线所做成的两个邻角中的任何一个,称作直线与平面的夹角,并记作![]() 。
。
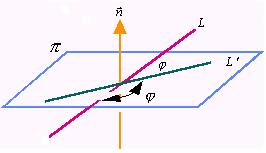
显然,这两个角互为补角,因此,我们不妨规定:![]()
下面导出![]() 的计算公式。
的计算公式。
设直线![]() 的方程为
的方程为
![]()
平面![]() 的方程为
的方程为
![]()
直线![]() 的方向向量
的方向向量![]() 与平面
与平面![]() 的法线向量
的法线向量![]() 的夹角为
的夹角为 ![]() 或
或 ![]() 。
。
而 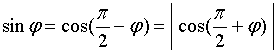
故  (5)
(5)
由(5)式有:
1、![]()
2、
五 平面束及其应用
平面束的概念
设直线![]() 由方程组
由方程组
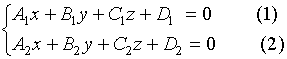
所确定,其中系数![]() 与
与![]() 不成比例,亦即由(1)、(2)所表示的两平面不平行。
不成比例,亦即由(1)、(2)所表示的两平面不平行。
建立三元一次方程
![]()
其中![]() 为任意常数。
为任意常数。
因![]() 与
与![]() 不成比例,对于任何一个
不成比例,对于任何一个![]() 值,方程(3)
值,方程(3)
![]()
的系数![]() 不全为零,从而(3)表示一个平面。
不全为零,从而(3)表示一个平面。
若一点在直线![]() 上,则点的坐标必同时满足方程(1)和(2),因此,也必满足(3),则方程(3)表示过直线的一个平面。而且对于不同的
上,则点的坐标必同时满足方程(1)和(2),因此,也必满足(3),则方程(3)表示过直线的一个平面。而且对于不同的![]() 值,方程(3)表示过直线的不同平面。
值,方程(3)表示过直线的不同平面。
反过来,通过直线![]() 的任何平面(除平面(2)外),都包含在方程(3)所表示的一族平面内。
的任何平面(除平面(2)外),都包含在方程(3)所表示的一族平面内。
通过定直线的所有平面的全体称为平面束,而方程(3)称为过直线![]() 的平面束方程。
的平面束方程。

【例2】求直线![]() :
:
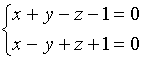
在平面![]()
![]()
上的投影直线![]() 的方程。
的方程。
【解一】直线![]() 在平面
在平面![]() 上的投影直线,也应在过
上的投影直线,也应在过![]() 且垂直于平面
且垂直于平面![]() 的平面上,而过直线
的平面上,而过直线![]() 的平面束方程为
的平面束方程为
![]()
即 ![]()
其中![]() 为任意常数。
为任意常数。
使它与平面![]() 相垂直条件为
相垂直条件为 ![]()
![]() ,
, ![]()
故,过直线![]() 且垂直于平面
且垂直于平面![]() 的平面为
的平面为
![]()
![]()
从而,投影直线的方程为
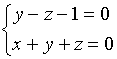
【解二】先给出直线![]() 的对称式方程
的对称式方程
令![]() ,解方程
,解方程 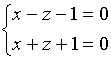 有
有 
得直线上的一点
![]()
直线的方向向量为
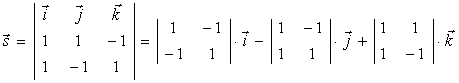
![]()
而平面的法线向量为
![]()
过直线![]() 且垂直于平面
且垂直于平面![]() 的方程可设为
的方程可设为
![]()
这里系数![]() 应适合方程
应适合方程

解之得

代入所设投影平面方程有
![]()
约去非零因子![]() , 得
, 得
![]()
投影直线的方程为